Optomechanical Realization of Bosonic Kitaev Chain

Core Concepts

Experimental realization of unique bosonic Kitaev chain dynamics.

Abstract

The content discusses the experimental realization of the bosonic Kitaev chain in a nano-optomechanical network. Key highlights include: Parametric interactions induce beam-splitter coupling and two-mode squeezing. Extraordinary phenomena in bosonic dynamics and transport. Quadrature-dependent chiral amplification and exponential gain scaling. Sensitivity to boundary conditions due to non-Hermitian topological nature. Topological phase transition and rich dynamical phase diagram exploration. Exponential enhancement of response to small perturbations. Establishment of a system for studying non-Hermitian topology and its applications.

Stats

"We report the experimental realization of its bosonic analogue in a nano-optomechanical network." "Finally, we present an experimental demonstration of an exponentially enhanced response to a small perturbation."

Quotes

"These results represent the demonstration of a new synthetic phase of matter whose bosonic dynamics do not have fermionic parallels."

Key Insights Distilled From

Optomechanical realization of the bosonic Kitaev chain - Nature

by Jesse J. Sli... at www.nature.com 03-27-2024

https://www.nature.com/articles/s41586-024-07174-w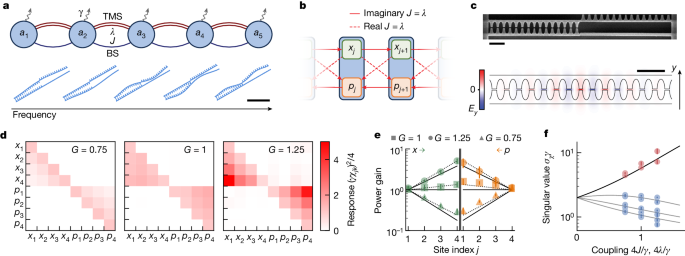

Deeper Inquiries

How does the bosonic Kitaev chain dynamics impact current understanding of topological phases

The dynamics of the bosonic Kitaev chain represent a significant advancement in our understanding of topological phases. By experimentally realizing the bosonic analogue of the fermionic Kitaev chain in a nano-optomechanical network, researchers have uncovered a new synthetic phase of matter with unique properties. The observation of quadrature-dependent chiral amplification, exponential scaling of gain with system size, and sensitivity to boundary conditions all point to the non-Hermitian topological nature of the bosonic Kitaev chain. These findings challenge conventional wisdom and expand the scope of topological phases beyond fermionic systems. The ability to probe topological phase transitions and establish a rich dynamical phase diagram further enhances our grasp of the intricate interplay between topology and bosonic dynamics.

What potential challenges or limitations might arise in applying these findings to real-world signal manipulation and sensing technologies

While the experimental realization of the bosonic Kitaev chain opens up exciting possibilities for signal manipulation and sensing technologies, several challenges and limitations must be considered. One potential challenge lies in scaling up the nano-optomechanical network to practical sizes for real-world applications. The exponential scaling of gain with system size, although advantageous for certain phenomena, may pose difficulties in maintaining control and stability in larger systems. Additionally, the strong sensitivity to boundary conditions could introduce complexities in implementing these findings in practical devices. Furthermore, the need for precise control over interaction phases and amplitudes to probe the topological phase transition may require sophisticated experimental setups, potentially limiting the widespread adoption of these techniques in signal manipulation and sensing technologies.

How can the study of non-Hermitian topology in this context influence advancements in other scientific fields

The study of non-Hermitian topology in the context of the bosonic Kitaev chain has the potential to influence advancements in various scientific fields beyond condensed matter physics. Understanding the unique properties of non-Hermitian topological phases could lead to novel applications in quantum information processing, where unconventional dynamics play a crucial role. By establishing a powerful system for studying non-Hermitian topology, researchers can explore new avenues for signal manipulation and sensing technologies that leverage the rich dynamical phase diagram of the bosonic Kitaev chain. These insights may also have implications for quantum computing, quantum communication, and other interdisciplinary areas where topological phases and non-Hermitian systems intersect.