Solving Tricky Python Puzzles: Unblocking Blocks and Minimizing Coins

Core Concepts

This article presents two challenging Python programming problems - an "Unblock Me" game and a Coin Change optimization problem. The author invites readers to demonstrate their Python expertise by solving these tricky coding challenges.

Abstract

The article presents two Python programming problems that test the reader's coding skills:

1. Unblock Me Puzzle:

   • The objective is to write Python code to represent a puzzle where a red block needs to be moved out of the map through the exit on the right.
   • Each block can only move in one direction parallel to its length, and blocks cannot pass through each other.
   • The task is to find the shortest possible way to solve the puzzle.

2. Minimum Number of Coins:

   • The goal is to write a Python function min_coins(target_value, coins) that determines the minimum number of coins required to achieve a target value.
   • The target_value is an integer, and the coins parameter is a list of coin denominations (e.g., [1, 2, 5]).
   • The author provides an example of min_coins(121, [1, 2, 5]), which should return the minimum number of coins needed to make 121.

The article challenges readers to demonstrate their Python programming skills by solving these tricky coding problems.

Stats

None

Quotes

None

Key Insights Distilled From

You’re A Python King If You Can Answer These 4 Very Tricky Questions

by Liu Zuo Lin at zlliu.medium.com 04-06-2024

https://zlliu.medium.com/youre-a-python-king-if-you-can-answer-these-4-very-tricky-questions-207caa22cdee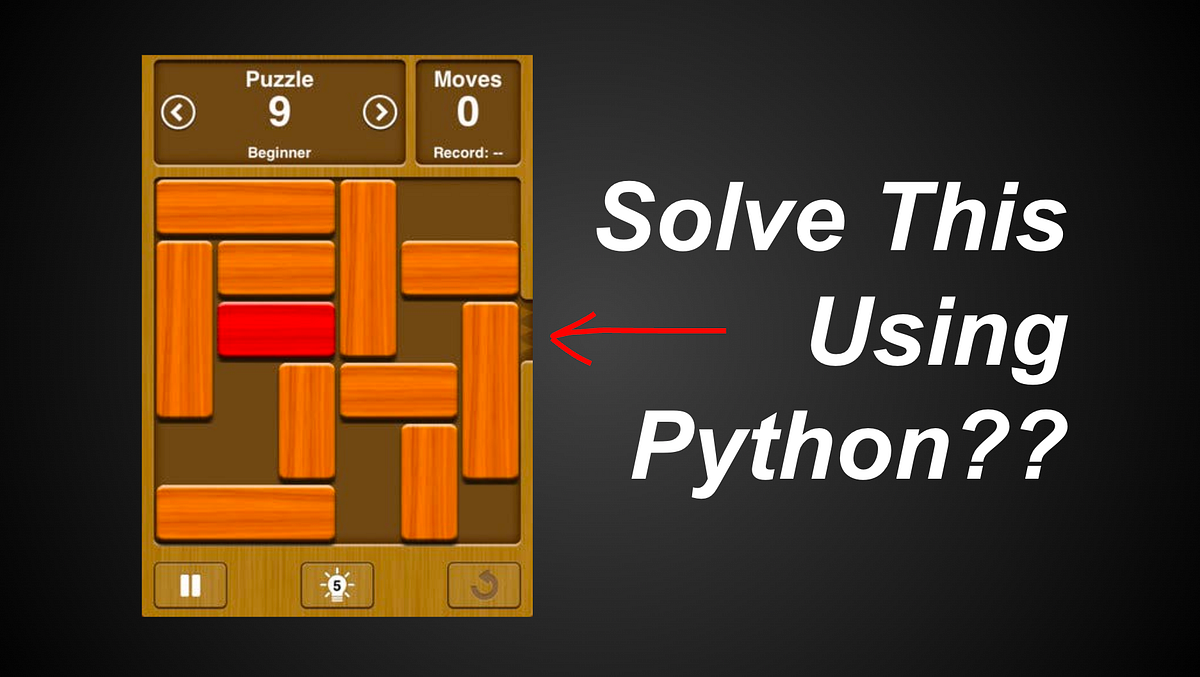

Deeper Inquiries

How can the "Unblock Me" puzzle be generalized to handle more complex board configurations and block arrangements?

To generalize the "Unblock Me" puzzle for more complex scenarios, we can introduce additional constraints and features. One way to do this is by allowing blocks to have different shapes and sizes, each with its own movement restrictions. This would require defining a more intricate data structure to represent the blocks and their interactions. Additionally, we could introduce obstacles on the board that blocks need to navigate around, adding another layer of complexity to the puzzle. By expanding the rules and possibilities, we can create a more challenging and engaging puzzle-solving experience.

What are the time and space complexity trade-offs of different approaches to solving the Coin Change problem?

In the Coin Change problem, different approaches like dynamic programming and greedy algorithms offer varying time and space complexity trade-offs.

Dynamic programming typically has a time complexity of O(target_value * len(coins)) and a space complexity of O(target_value), making it efficient for larger target values but requiring more memory.
Greedy algorithms, on the other hand, have a time complexity of O(target_value * len(coins)) but a space complexity of O(1), making them more memory-efficient but potentially less optimal in finding the minimum number of coins for certain cases.
Choosing the right approach depends on the specific requirements of the problem at hand, balancing between time efficiency and space utilization.

How could the Coin Change problem be extended to include additional constraints, such as a limited number of each coin denomination?

To extend the Coin Change problem with constraints like a limited number of each coin denomination, we can modify the existing algorithms to account for these limitations. One approach is to incorporate a count for each coin type, ensuring that the algorithm considers the availability of coins during the calculation. This would involve updating the dynamic programming or greedy algorithm to track the remaining count of each coin denomination as coins are used. By enforcing these constraints, we can create a more realistic scenario that reflects practical limitations in coin usage.