Understanding Shapes on Different Curved Surfaces

核心概念

The author explores how the curvature of surfaces impacts the number of sides shapes with straight sides and 90-degree angles can have, challenging the traditional definition of a square.

摘要

On flat surfaces like the Euclidean plane, shapes with equal side lengths and 90-degree angles must have four sides, but on curved surfaces like spheres or pseudospheres, this rule changes. Positive curvature allows for shapes with fewer than four sides, while negative curvature enables shapes with more than four sides. The concept of Gaussian curvature helps understand how different surfaces affect geometric properties.

統計資料

A sphere has positive Gaussian curvature at every point.
A saddle shape has negative Gaussian curvature.
The angles of a triangle drawn on a shape with positive curvature add up to more than 180 degrees.
On a sphere, a shape with three sides can be created with equal side lengths and 90-degree angles.
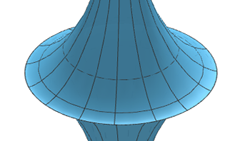
On a pseudosphere (negative curvature), a five-sided shape can be formed with straight sides and 90-degree angles.

引述

"It all depends on the curvature!"
"The positive or negative curvatures of surfaces impact the geometric properties of shapes."

從以下內容提煉的關鍵洞見

What is a square?

by 於 plus.maths.org 02-26-2024

https://plus.maths.org/content/what-square

深入探究

How does understanding geometry on curved surfaces impact real-world applications?

Understanding geometry on curved surfaces has significant implications for various real-world applications. For instance, in architecture and engineering, where structures are often designed to fit non-planar surfaces like domes or spheres, knowledge of curved geometries is crucial. By incorporating principles of Gaussian curvature and non-Euclidean geometries, architects and engineers can create more efficient and aesthetically pleasing designs that account for the inherent curvature of the surface.
Moreover, in fields such as cartography and geodesy, which deal with mapping the Earth's surface or other planetary bodies, understanding geometry on curved surfaces is essential. By applying concepts from spherical trigonometry and geodesics, accurate maps can be created that represent the true distances and angles between points on a curved surface.
Overall, a deep comprehension of geometry on curved surfaces enhances problem-solving abilities in various practical scenarios by providing insights into how shapes behave in three-dimensional space beyond traditional Euclidean geometry.

Could there be exceptions to the rules observed in this article based on specific surface characteristics?

While the rules discussed in the article hold true for general cases involving surfaces with constant Gaussian curvature at every point (such as spheres or pseudospheres), exceptions may arise when dealing with surfaces exhibiting varying curvatures across different regions.
For instance, if a surface has regions with mixed positive and negative curvatures or areas where the curvature changes abruptly due to irregularities or singularities, traditional geometric rules may not apply uniformly. In such cases, unique properties related to differential geometry come into play to describe how shapes behave under varying curvatures.
Additionally, exotic geometries like fractal curves or manifolds with non-smooth properties could introduce exceptions to standard geometric rules observed on smooth continuous surfaces. These exceptional cases challenge conventional notions of shape representation and require specialized mathematical tools to analyze their geometric properties accurately.

How does exploring non-Euclidean geometries influence mathematical problem-solving techniques?

Exploring non-Euclidean geometries opens up new avenues for mathematical problem-solving techniques by expanding beyond the constraints of Euclidean space. Non-Euclidean geometries provide alternative frameworks for analyzing spatial relationships that deviate from classical axioms established by Euclid.
By delving into hyperbolic or elliptic geometries characterized by negative or positive Gaussian curvatures respectively,
mathematicians gain deeper insights into complex geometric structures that exhibit unconventional behaviors compared to flat Euclidean spaces.
These explorations lead to novel problem-solving strategies tailored towards addressing challenges posed by non-traditional geometric settings.
Furthermore,
the study of non-Euclidean geometries fosters creativity
and innovation within mathematics
by encouraging mathematicians
to think outside conventional boundaries
and develop new approaches
for tackling problems across diverse disciplines.
Ultimately,
exploring these alternative geometrical systems enriches mathematical reasoning skills
and broadens problem-solving capabilities through exposure
to a wider spectrum
of geometric possibilities beyond Euclid's classical framework.